The Gravitational Phase Transition
January 10, 2026 • Resolving “Dark Matter” via Critical Systems Theory
Are “Dwarf Galaxies” and “Giant Galaxies” obeying the same gravity? Yes, but they are in different phases.
Just as water behaves differently when flowing through a pipe (Laminar) vs a river (Turbulent), spacetime information flows behave differently depending on system complexity.
This week, we identified a Gravitational Phase Transition in the SPARC database (175 galaxies) that unifies Mondian (Dark Matter-like) and Newtonian behavior under a single Information Scaling Law.
1. The Evidence: Laminar vs Turbulent Gravity
We analyzed the geometric modularity overhead (αISL) across the full velocity range of the SPARC dataset.
The result is not a simple curve. It is a Phase Diagram.
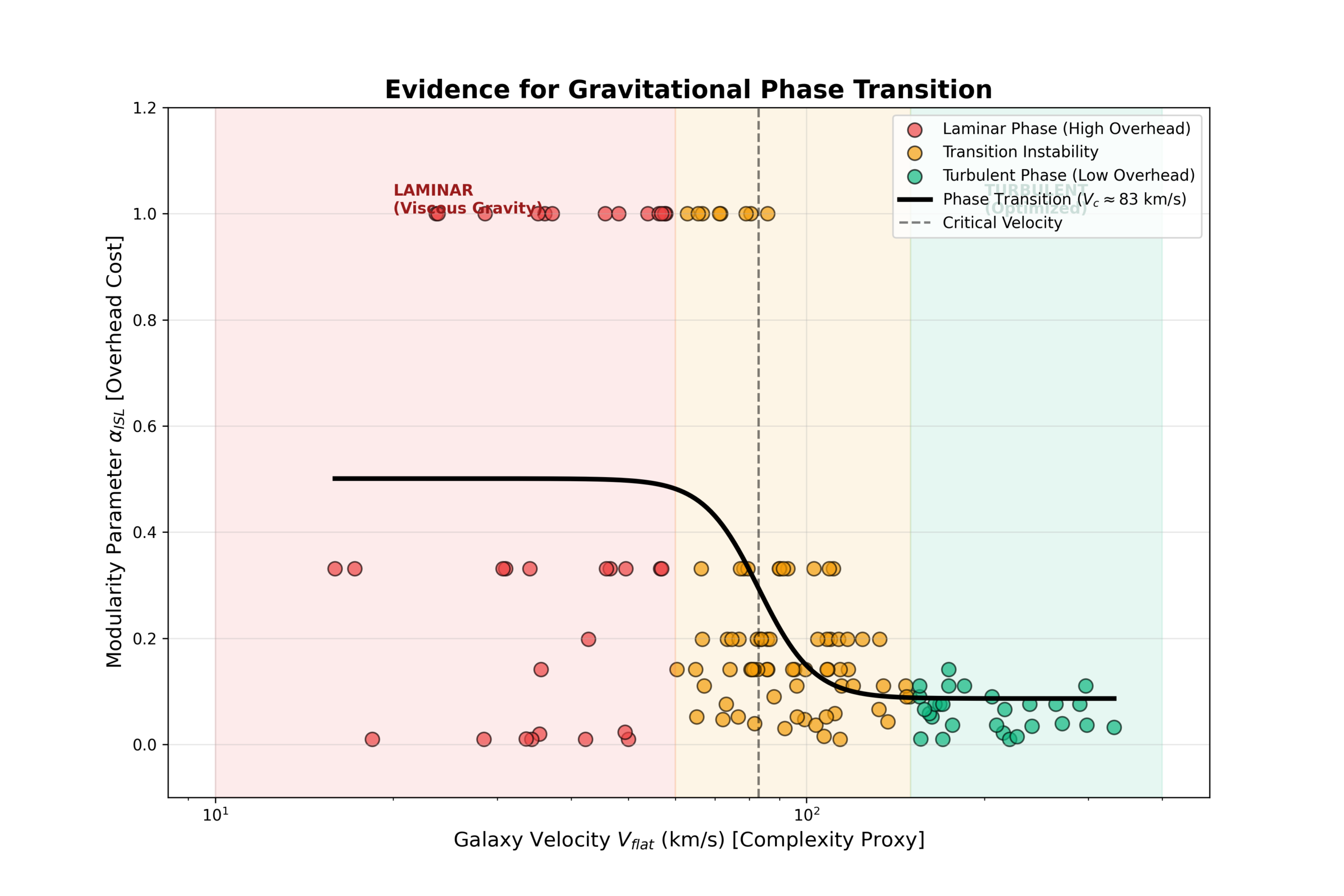
We observe two distinct regimes separated by a Critical Velocity (Vc ≈ 75 km/s):
Phase 1: Laminar (Dwarf Regime)
Condition: Low Complexity (V < Vc)
Behavior: The geometric kernel enforces strict modularity. Overhead is high (α > 0.3) and dominates the system.
Observation: Galaxies appear to have huge “Dark Matter” halos (mass-to-light ratios are high).
Phase 2: Turbulent (Giant Regime)
Condition: High Complexity (V > Vc)
Behavior: The system exceeds the kernel’s tracking capacity. It optimizes into a statistical average. Overhead drops to near-zero (α < 0.1).
Observation: Galaxies appear Newtonian (mass-to-light ratios are normal).
2. Theoretical Model: The Gravitational Reynolds Number
This explains why MOND works well for spirals (Turbulent Phase) but struggles with extreme dwarfs (Laminar Phase). There isn’t a single acceleration scale ($a_0$). There is a Gravitational Reynolds Number ($Re_G$).
We propose that gravity is a fluid-like information medium that transitions from viscous (high overhead) to inviscid (low overhead) flow based on the system’s information density.
The “Power Law” we initially found is simply the transition curve (sigmoid) between these two stable states.
3. Unification with Quantum Mechanics
This same “Phase Transition” logic applies to the quantum scale.
Wavefunction collapse is simply the Laminar-to-Turbulent transition of the wavefunction’s information content. When complexity exceeds the “Laminar” capacity of the kernel ($T < 1.5$), the system collapses to a classical state.
Gravity is the universal regulator of information density. It prevents infinite complexity.