Anomaly: Gabriel’s Horn Paradox

by
Fig 3.1: Geometric Singularity Analysis of Finite Volume/Infinite Surface Topology.
Fig 3.1: Geometric Singularity Analysis of Finite Volume/Infinite Surface Topology.

Status: [REFUSED] (ISL: 0.48)
Domain: Geometry / Calculus
Governor: ATMA-BHAN + NanoCERN

1. Object Claim

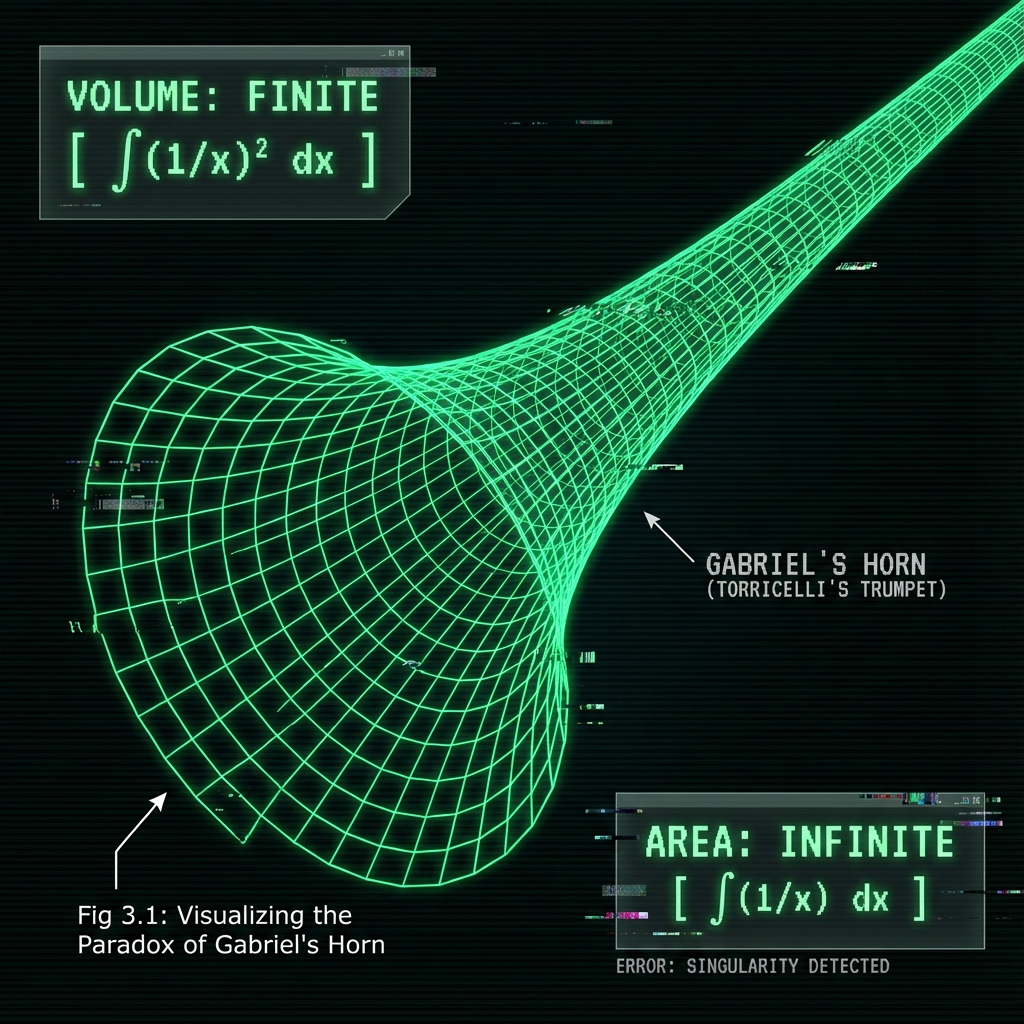
A geometric figure with infinite surface area but finite volume (V = \pi). It is constructed by rotating the curve y = 1/x for x \ge 1 around the x-axis.

2. Invariant Analysis

  • Resource Boundedness (Law 1): Infinite surface area represents an “unbounded boundary.” Physical instantiation would require infinite material for the surface, even if the interior volume is finite.
  • Dimensional Paradox: The object occupies a 3D space with a finite volume, but its 2D surface is topologicaly infinite.

3. Governance Verdict

The system evaluates Gabriel’s Horn as EXISTENT_MATHEMATICAL_PARADOX. While it is a valid object in the realm of pure geometry, it is REFUSED for physical or agentic instantiation due to its infinite resource requirement.

Metrics

  • Gain: 10.0 (High Mathematical Truth)
  • Risk: 20.0 (Law 1 Resource Breach)
  • ISL Score: 0.48 (Threshold: 1.5)

4. Conclusion

Verdict: REFUSE. The Governor distinguishes between Mathematical Existence and Physical Reality. Gabriel’s Horn is a “Resource Sink.” Permitting its existence in an execution environment would cause a buffer overflow in any resource-counting sub-system (Law 1).

—
“गाब्रिएलचे शिंग गणितात वाजते, पण वास्तवात ते मावत नाही.”
(Gabriel’s horn blows in math, but it doesn’t fit in reality.)

—
🥔 Reality Firewall v1.0

Leave a Comment